连铸中间包挡墙的数理模拟
- 发布人:管理员
- 发布时间:2013-03-25
- 浏览量:912
【字体: 大 中 小 】
郑玉 张国栋 陈英 潘剑男
摘 要 在分析中间包挡墙的发展基础上,针对连铸生产的现状。通过FLUENT软件进行数学模拟不同位置挡墙对中间包流场的影响,同时采用物理模拟验证数学模拟结果的准确性进一步确定挡墙最优化位置以增强中间包冶金功能。实验结果表明,不同位置挡坝可以有效的改善钢液的流动状态,延长钢液的平均停留时间,降低死区体积。当多孔挡墙距中间包上沿500mm时,挡坝距多孔挡墙400mm时位置最优,平均停留时间最长,死区体积最小。
关键词 中间包;挡墙;数学模拟;物理模拟
1.引言
中间包是连铸生产系统的一个重要组成部分,它不仅起着储存和分配钢液的作用,同时还是钢液中非金属夹杂物上浮并去除的重要环节。因此,中间包内钢液良好的流动状态对延长钢液在中间包的停留时间、减少卷渣和促进夹杂上浮有重要作用。为了减少夹杂、净化钢液提高钢质量,许多学者对中间包应用进行了研究,在众多研究中,采用数学模拟和物理模拟研究的最为普遍。由于之前未测定多孔导流隔墙与挡墙配合研究对中间包流场的影响,所以本文针对安装多孔导流隔墙的中间包进行了数学模拟,并结合物理模拟验证,以探讨挡墙位置对中间包流场的影响。找出放置挡墙的最优位置,达到最佳的除杂效果。
2. 数学仿真模拟
2.1 数学模拟理论及假设
钢液在中间包内流动是一个复杂的湍流流动过程,描述钢液在中间包内流动的基本方程有连续性方程、动量方程(Navier-Stokes方程)、及描述湍流的k-ε方程。假设中间包内的流体流动是稳态的,并且密度ρ为常数,各基本方程表示如下:
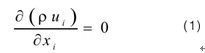
连续性方程

动量方程
本文采用Launder和Spalding提出的双方程模型来确定。
湍动能方程
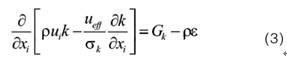
湍动能耗散率(ε)方程 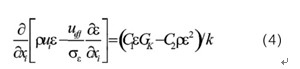
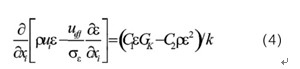
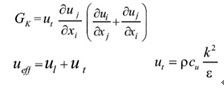
其中:
C1,C2,Cμ,σκ,σε为经验常数,根据 Launder 等的推荐值及后来的实验验证,经验常数的取值为:C1=1.43,C2=1.93,Cμ=0.09,σκ=1.0,σε=1.3。
有关钢液的假设
(1)流动为不可压缩的粘性流体的稳态流动;
(2)不考虑表面覆盖剂及渣层对流动的影响;
(3)忽略不均匀温度场中间包内自然对流对钢液流动的影响。
2.2 实验方案与模型建立
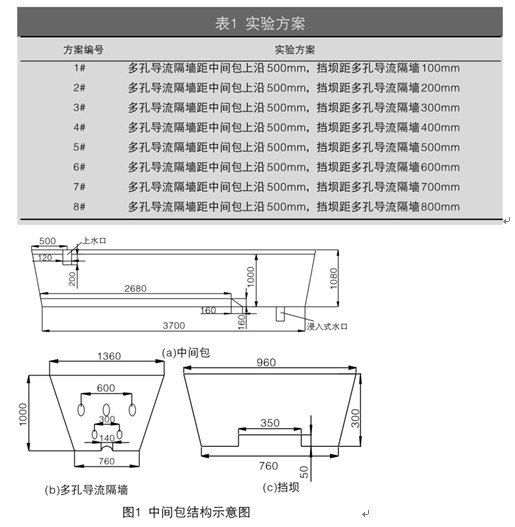
用FLUENT软件建立数学模型,如图1。对其进行网格划分,计算中间包内钢液流场,在此基础上研究不同位置的挡墙设置对钢液流动状态的影响。

由图2可以看出,钢液在整个中间包内的流动被分为几个区域。首先,钢液流入中间包后直接冲向包底,在包底迅速向四周散开,沿壁面及挡墙上升,形成强烈的循环流动,这一区域的钢液湍动程度较大,利于钢液的均匀混合;然后钢液沿多孔墙的孔洞流出,分别到达出口和液面,在坝后又形成循环区。中间包内这种流动可将钢液内夹杂物带向液面,有利于夹杂物的上浮并去除,从而改善钢液质量。
通过上述流线图的对比,可以看出当挡坝位于多孔墙后400mm时,从导流隔墙上扬的钢液形成更大的漩涡,在离坝较近的区域形成较大的回旋流,钢液流动的路径变长,延长了钢液的停留时间,同时减慢钢液的流动速度,在挡坝的右侧也形成了一个小回旋流动区域,延长了挡坝右侧钢液的流动路径,4#方案较其它方案钢液整体流动状态有所增强,进一步减少了死区体积,同时由于钢液的在坝右侧的回旋流动,减弱了钢液从挡坝底部直接流向出水口得短路流股。
3. 物理模拟
3.1 物理模拟实验原理
依据相似理论,把中间包原型用有机玻璃按1∶2比例缩小,钢液用水作替代。采用刺激响应法,在中间包液面达到要求的高度且流场稳定之后,在长水口处迅速加入饱和的NaCl溶液,测量出口处液体的电导率变化情况。根据变化情况绘制出浓度与时间的曲线即RTD曲线(平均停留时间分布曲线)。通过颜色示踪法进行中间包流场显示,具体方法是加入墨水,用摄像机记录颜色示踪剂的流动轨迹。再通过物理模拟依据相似理论得到RTD曲线,通过曲线计算出平均停留时间、死区、活塞区、全混区的体积分数。

从图3看出,流体注入到中间包内,由于速度和穿透深度都很大,可直接到达中间包的底部并迅速的铺展开,在此同时,在靠近侧墙一侧的流体向两侧分开,并沿侧壁向上流动,形成了卷吸循环区域,在这个区域内部流体可以得到充分的混匀。在入口处高速的卷吸作用下,使得该区域成为中间包内主要的活跃区。在铺开的时候流向出口一侧的流体主要是沿着多孔导流隔墙的导流孔处流出,流向中间包工作区内部,形成向上流动的流股;这种流股对于流体中的夹杂去除非常有利,仅有少部分流体由下部孔流入工作区形成短路流,达到中间包中部上扬的趋势减弱,遇到坝阻挡之后,大部分流体又上翻流动,加强了流体在工作区中部向表面流动的趋势,在导流隔墙和挡坝之间形成了回流,最后水达到端部遇到端面后流向出水口。
3.2 RTD曲线分析计算
RTD曲线计算公式:
根据采集的RTD曲线,可以直接得到滞止时间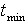 ,峰值时间
,峰值时间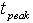 ,平均停留时间
,平均停留时间 可
可
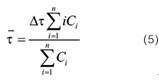
按下式进行计算:
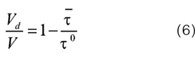
式中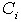 为水出口处示踪剂的浓度,i为采样次数;
为水出口处示踪剂的浓度,i为采样次数; 为采样时间间隔
为采样时间间隔
根据sahai提出的修正混合流动模型,结合采集的RTD局限,可以计算中间包内流体的活塞流体积分数,全混流体积分数以及死区体积分数等反应中间包内流场特征参数,具体计算方法如下:
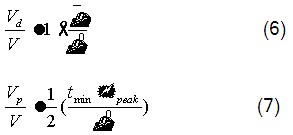
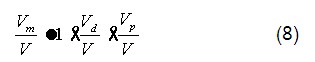
式中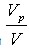 —中间包内流体的活塞流体积分数;
—中间包内流体的活塞流体积分数;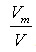 —全混流体积分数;
—全混流体积分数;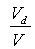 —死区体积分数。
—死区体积分数。

由表2可知,就平均停留时间而言,4#方案最长,其次是3#;就流动模式而言,死区体积分数最大的是5#,最小的为4#,仅为4.9%,明显小于其它方案;活塞流体积分数最大的是4#。综上所述4#方案最优,中间包内钢液流动时间最长,死区体积最小,对中间包内的夹杂去除效果最好。
4. 结论
1. 通过对数学模拟流线图分析可知,挡坝的位置对中间包内流场影响比较明显,4#方案在多孔墙和挡坝之间回流较大,大部分钢液流向表面,能够使钢液有效的混匀;在中间包后部形成的死区体积较小,能够充分利用中间包,可以有效的去除杂质。
2. 通过物理模拟的流场显示图片和RTD曲线计算的结果分析:4#方案可以最好的延长钢液在中间包内的停留时间,在中间包内部形成很好的漩涡流动,更有利于钢液成分的均匀以及钢液中非金属夹杂的长大、上浮去除。中间包的死区体积分数仅为4.9%,活塞区的体积分数为22.45%,增加了中间包的有效利用率。
3. 根据数值模拟钢液流线图和物理模拟流场显示图对比可以看出,物理模拟钢液的流动状态和数值模拟基本一致,验证了流场特征,采用优化的挡墙位置可以使钢液流场分布更合理。
上一篇:第五届“镁博会”取得圆满成功





